Diving into the statistics of PCR test technology
One of the claims stated by supporters of the Covid regime is that C cases were underreported and that official statistics do not reflect reality (see here or here). I agree with the latter part of the claim, but in this article I will show why the claim that Covid numbers are underreported is not true and why, in fact, the official statistics overstate the actual prevalence of C-19.
Multiple factors can be identified that distorted the data, for instance, the financial incentives for hospital administrators to falsely classify different death causes as C-19. Other factors included testing practices of health authorities or their reporting policies. However, one of the most important factors, which distorted the data and overstated Covid numbers, was a statistical effect related to what epidemiologists call pretest probability - a problem caused by randomly testing large parts of a population with a low infection rate.
The role of pretest probability
Imagine we test a population of 100,000 males using a pregnancy test with an error rate of 1 %. In such a scenario we would get 1,000 men who tested positive for pregnancy - a result that is obviously nonsense. What this simple example shows is that our knowledge about the prevalence of male pregnancies among the general tested population (pretest probability = 0 %) allows us to conclude that 100% of all positive tests are false positive.
But let’s take a step back. The accuracy of PCR tests is measured by two performance indicators: sensitivity and specifity. These two indicators are not unique to PCR tests. If you are a machine learning engineer, you might have come across these indicators during the performance evaluation of any classification algorithm.
In the case of PCR tests the sensitivity reflects the amount of people among actually infected people, who get a correct positive test. For instance, a sensitivity of 99 % means that (statistically) 99 out of 100 actually infected individuals get a correct positive test, 1 out of these 100 gets a false negative test result.
The second performance indicator is the specifity, which reflects the amount of people among non-infected people, who get a correct negative test. For instance, a specifity of 99 % means that (statistically) 99 out of 100 non-infected people get a correct negative test, 1 non-infected individual gets a false positive test.
A PCR test with a sensitivity and specifity of 99% is a highly accurate test. The problem, however, was how authorities used PCR tests, deploying these tests at a massive scale and randomly testing a large population with only a tiny fraction of actually infected individuals.
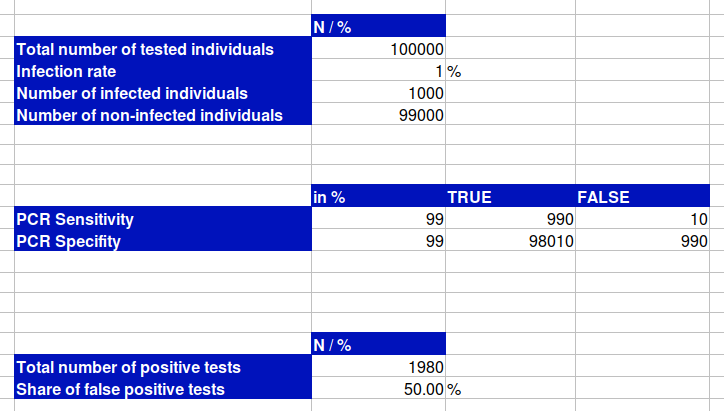
Let's assume we test a cohort of 100,000 people with an infection rate of 1 %, which means that 1,000 people would be actually infected, using a PCR test with a sensitivity and specifity of 99 %. A sensitivity of 99 % would mean that out of these 1,000 infected people we would get 990 correct positive tests and 10 infected individuals, who get a false negative test.
The problem is caused by the specifity. We do not only test the 1,000 actually infected people, we also test the 99,000 people, who are not infected. Out of these 99,000 non-infected people we get 98,010 people with a correct negative test, but at the same time we get 990 false positive tests. In sum, we would get 1,980 positive tests, of which 50 % are false positive.
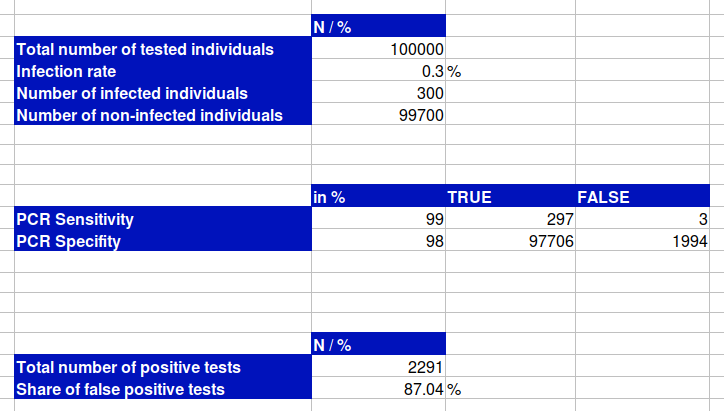
It becomes worse when we assume a more realistic scenario and reduce the infection rate from 1 % to 0.3 %. In this case, the share of false positives would be 77.05 % and if we additionally reduce the specifity from 99 % to 98 %, which is also more realistic, 87.04 % of all positive tests would be wrong.
Imagine this: take all the numbers that the media has publicly stated and subtract between 50 % and 90 %. At least half of the positive tests, if not more, were statistically "hallucinated" - to borrow a term from AI.
In epidemiology this statistical effect is related to the so-called pre-test probability, stating that the higher the prevalence of a disease, the higher the probability of a positive PCR test being correct. The lower the infection rate, the less likely is a correct positive test.
PRC tests with a sensitivity and specifity of 99% or 98 % are highly accurate tests, the problem though was how authorities used those tests. The main contributing factor is the infection rate. Randomly testing a large population with a low infection rate results in a high amount of false positives among positive tests. If you test only sick people with flu-like symptoms, this amount would arguably be much lower.
The problems of 2-step procedures
Another problem that should be discussed is the role of PCR tests based on 2-step procedures. A 2-step procedure describes a PCR test that looks for two gene sequences. What needs to be considered here is that there are two different types of 2-step procedures: specific and non-specific procedures.
Specific PCR tests look for two gene sequences and give a positive result, only if it found both gene sequences. If it detected one gene sequence, the test would be invalid, if it didn't find any gene sequence the test would be negative. This results in:
1+1 = positive
1+0 / 0+1 = inconclusive
0+0 = negative
In the case of unspecific 2-step procedures, the PCR test looks for two gene sequences, too, but it already results in a positive test if it only found one gene sequence:
1+1 = positive
1+0 / 0+1 = positive
0+0 = negative
The problem with non-specific 2-step procedures is that the error rates for both gene sequence are adding up. If a test had an error rate of 2% for the 1st gene sequence and an error rate of 3% for the 2nd gene sequence, we get a total error rate of 5%.
I mention this because the WHO recommended non-specific PCR tests, at least at the beginning of the pandemic, which might have further inflated the numbers.
Conclusion
The concept of pretest probability shows us that testing a large populations with a low infection rate results in a high share of false positive tests among positive tests, ranging from 50 to 90% practically speaking. Don't get me wrong, PCR is a fascinating technology that is useful as a tool among others to diagnose a disease or to analyze gene sequences. But the problem was how health authorities used those tests. Testing a large population with a low infection rate naturally results in a high share of false positive tests among all positive tests - this is not a conspiracy theory, but a mathematical fact.