Wie PCR-Tests die Corona-Zahlen inflationierten
Eine der Behauptungen der Befürworter des Covid-Regimes ist, dass die Anzahl der Covid-Fälle unterschätzt werden und die offiziellen Statistiken die Realität nicht widerspiegeln (siehe hier oder hier). Ich stimme dem zweiten Teil dieser Aussage zu, aber in diesem Artikel werde ich darlegen, warum die Hypothese, dass die Covid-Zahlen unterschätzt seien, grob irreführend ist und warum die offiziellen Statistiken in Wirklichkeit die tatsächliche Prävalenz von Covid-19 überschätzen.
Tatsächlich lassen sich mehrere Faktoren identifizieren, die die Daten verzerrten. Einer davon waren finanzielle Anreize für Krankenhausverwalter, verschiedene Todesursachen fälschlicherweise als Covid-19 zu klassifizieren. Weitere Faktoren waren die Testpraktiken der Gesundheitsbehörden oder deren Berichterstattungsrichtlinien. Einer der wichtigsten Faktoren jedoch, der die Daten verzerrte und die Covid-Zahlen inflationierte, war ein statistischer Effekt, der mit der sogenannten Pretest-Wahrscheinlichkeit zusammenhängt – ein Problem, das durch das wahllose Testen großer Teile der Bevölkerung mit einer niedrigen Infektionsrate zustande kam.
Die Rolle der Pretest Wahrscheinlichkeit
Man stelle sich vor, wir testen eine Population von 100.000 Männern mit einem Schwangerschaftstest, der eine statistische Fehlerquote von 1 % aufweist. In einem solchen Szenario würden 1.000 Männer ein positives Testergebnis für eine Schwangerschaft erhalten – ein offensichtlich unsinniges Ergebnis. Dieses einfache Beispiel zeigt, dass unser Wissen über die Prävalenz männlicher Schwangerschaften in der allgemeinen Bevölkerung (Pretest-Wahrscheinlichkeit = 0 %) uns erlaubt, zu dem Schluss zu kommen, dass 100 % aller positiven Tests falsch positiv sind. Ein ähnliches Problem hatten wir bei den Covid-19-Tests.
Aber lassen Sie mich einen Schritt zurückgehen. Die Genauigkeit von PCR-Tests wird üblicherweise durch zwei Leistungsindikatoren gemessen: die Sensitivität und Spezifität. Diese beiden Indikatoren sind nicht einzigartig für PCR-Tests. Wer schon mal Machine Learning Algorithmen entwickelte, sollte mit diesen beiden Performance Indikatoren bereits vertraut sein, da diese für die Evaluierung von Klassifikationsalgorithmen eingesetzt werden.
Im Falle von PCR-Tests gibt die Sensitivität an, wie viele Personen unter den tatsächlich infizierten Personen ein korrekt positives Testergebnis erhalten. Eine Sensitivität von 99 % bedeutet beispielsweise, dass (statistisch gesehen) 99 von 100 tatsächlich infizierten Personen ein korrekt positives Testergebnis erhalten, während 1 von 100 ein falsch negatives Testergebnis bekommt.
Der zweite Performance Indikator ist die Spezifität, die angibt, wie viele Personen unter den nicht infizierten Personen ein korrekt negatives Testergebnis erhalten. Eine Spezifität von 99 % bedeutet beispielsweise, dass (statistisch gesehen) 99 von 100 nicht infizierten Personen ein korrekt negatives Testergebnis erhalten, während 1 von 100 ein falsch positives Testergebnis bekommt.
Ein PCR-Test mit einer Sensitivität und Spezifität von 99 % ist ein sehr exakter Test. Das Problem bestand jedoch darin, wie die Gesundheitsbehörden PCR-Tests eingesetzt haben – nämlich das wahllose Testen einer großen Population mit nur einem kleinen Bruchteil tatsächlich infizierter Personen.
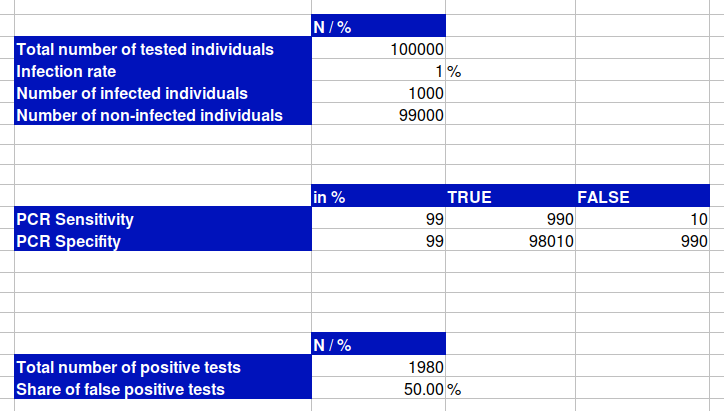
Nehmen wir an, wir testen eine Kohorte von 100.000 Personen mit einer Infektionsrate von 1 %, was bedeutet, dass 1.000 Personen tatsächlich infiziert wären, und verwenden dabei einen PCR-Test mit einer Sensitivität und Spezifität von 99 %. Eine Sensitivität von 99 % würde bedeuten, dass von diesen 1.000 infizierten Personen 990 ein korrekt positives Testergebnis erhalten und 10 infizierte Personen ein falsch negatives Testergebnis.
Das Problem entsteht durch die Spezifität. Wir testen nicht nur die 1.000 tatsächlich infizierten Personen, sondern auch die 99.000 nicht infizierten Personen. Von diesen 99.000 nicht infizierten Personen erhalten 98.010 ein korrekt negatives Testergebnis, aber gleichzeitig 990 ein falsch positives Testergebnis. Insgesamt hätten wir 1.980 positive Tests, von denen 50 % falsch positiv wären.
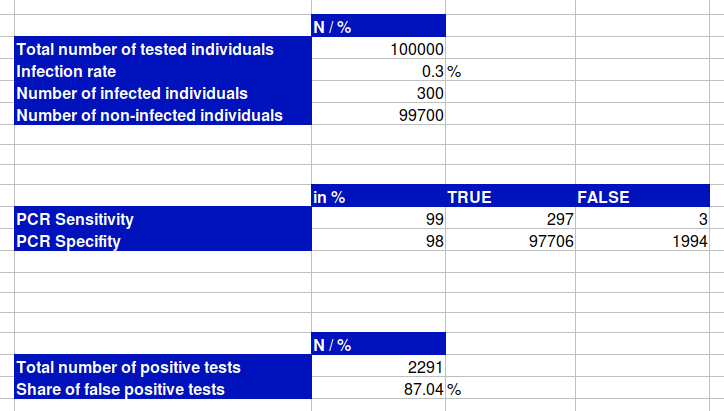
Der Anteil der falsch positiven Tests an der Gesamtzahl der positven Tests wird noch höher, wenn wir eine realistischere Infektionsrate von 0,3 % annehmen, anstatt 1 %. In diesem Szenario läge der Anteil der falsch positiven Ergebnisse bei 77,05 %. Reduzieren wir zusätzlich die Spezifität von 99 % auf 98 % (ebenfalls realistischer), wären 87,04 % aller positiven Tests falsch.
Dieses Beispiel zeigt, dass die Zahlen, die in den öffentlichen Medien veröffentlicht wurden, ein Betrug waren und zwischen 50 % und 90 % abgezogen werden müssten.
In der Epidemiologie wird dieser statistische Effekt mit der sogenannten Prätest-Wahrscheinlichkeit in Verbindung gebracht, die besagt, dass die Wahrscheinlichkeit, dass ein positiver PCR-Test korrekt ist, mit der Prävalenz der Krankheit steigt. Je niedriger die Infektionsrate, desto geringer ist die Wahrscheinlichkeit, dass ein positiver Test korrekt ist.
PCR-Tests mit einer Sensitivität und Spezifität von 99% oder 98% sind sehr genaue Tests, das Problem allerdings war wie die Gesundheitsbehörden die Tests in der Praxis einsetzten. Der primäre Einflussfaktor, der die Corona-Zahlen inflationierte, war die niedrige Infektionsrate. Das wahllose Testen einer großen Population mit niedriger Infektionsrate führte zu einer hohen Anzahl an falsch-positiven Tests unter der Gesamtzahl der positiven Tests. Würde man nur Personen testen, die Grippe-ähnliche Symptome aufweisen, wäre die Falsch-Positiv-Rate wesentlich geringer.
Das Problem der zweistufigen Verfahren
Ein weiteres Problem, das ich bei meine Recherche entdeckte, betrifft die Rolle von PCR-Tests, die auf zweistufige Verfahren basieren. Bei einem zweistufigen Verfahren sucht der PCR-Test nach zwei Gensequenzen. Es gibt jedoch zwei unterschiedliche Typen solcher Verfahren: spezifische und unspezifische Verfahren.
Bei spezifischen Verfahren sucht der PCR-Test nach zwei Gensequenzen und ergibt dann ein positives Ergebnis, wenn beide Gensequenzen in der Probe gefunden werden. Besteht nur mit einer Gensequenz eine Übereinstimmung, ist das Ergebnis ungültig, besteht überhaupt keine Übereinstimmung ergibt sich ein negatives Ergebnis. Daraus ergibt sich:
1+1 = positiv
1+0 / 0+1 = ungültig
0+0 = negativ
Im Falle der unspezifischen zweistufigen Verfahren sucht der PCR-Test auch nach zwei Gensequenzen, allerdings ergibt sich bereits ein positives Ergebnis wenn nur eine Gensequenz gefunden wird. Daraus ergibt sich:
1+1 = positiv
1+0 / 0+1 = positiv
0+0 = negativ
Das Problem bei unspezifischen Verfahren ist, dass sich die Fehlerraten der einzelnen Gensequenzen addieren. Hat ein Test eine Fehlerrate von 2 % für die erste Gensequenz und 3 % für die zweite Gensequenz, ergibt sich eine Gesamtfehlerrate von 5 %.
Die WHO empfahl zu Beginn der Pandemie sogenannte unspezifische Tests, was die Zahlen zusätzlich aufblähte. Gleichzeitig wurde suggeriert, dass zweistufige Verfahren zu genaueren Tests führen, was bei unspezifischen Verfahren nicht stimmt.
Konklusio
Die Behauptung, dass Covid-19-Fälle unterschätzt wurden, ignoriert die Rolle der Pretest-Wahrscheinlichkeit und deren Einfluss auf das Testen großer Populationen. Nicht falsch verstehen – PCR ist eine faszinierende Technologie, die als Werkzeug zur Krankheitsdiagnose oder zur Analyse von Gensequenzen in der Evolutionsbiologie genutzt werden kann. Das Problem war jedoch, wie Gesundheitsbehörden diese Tests einsetzten. Das Testen großer Populationen mit einer niedrigen Infektionsrate führt zu einem hohen Anteil falsch positiver Tests unter den positiven Ergebnissen. Dies ist keine Verschwörungstheorie, sondern eine mathematische Tatsache.